Rhif
Ffracsiynau a chanrannau
Mae ffracsiynau a chanrannau’n cynrychioli rhan o rif cyfan. Gallwn eu defnyddio i gynyddu neu leihau gwerth yn ôl cyfran benodol.

Cymhareb
Mae cymhareb yn dangos y berthynas rhwng dau werth. Gallan nhw fod mewn cyfrannedd union ac yn cynyddu wrth i'r llall gynyddu neu mewn cyfrannedd gwrthdro; mae un yn cynyddu wrth i'r llall leihau.

Amserlenni
O gynllunio taith ar fws neu drên i drefnu beth i'w wylio ar deledu neu archebu gwyliau haf, mae amserlenni yn ein helpu i ganfod ein ffordd drwy’r byd ac i gynllunio ein hamser.

Cyllid personol
Trwy agor dy gyfrif banc dy hun neu drwy reoli dy arian yn llwyddiannus, byddi’n dysgu sut i ymdrin â dy gyllid personol yn ofalus a sicrhau dy fod yn gallu rheoli ad-daliadau ar fenthyciadau.

Cyllid y cartref
Gall prynu neu rentu cartref fod yn dasg ddrud. Bydd meddwl am y fathemateg y tu ôl i gyllid y cartref yn dy helpu yn y dyfodol pan fyddi di'n symud i mewn i dy eiddo dy hun.

Newid canrannau
Gallwn ddefnyddio canrannau i gynyddu neu leihau swm mewn perthynas â’i faint, ee siopau’n tynnu canran oddi ar eu prisiau a’r llywodraeth yn cynyddu cost nwyddau trwy ychwanegu treth ganrannol.

Arian tramor a chyfraddau cyfnewid
Pan fyddi di’n mynd dramor, bydd yn rhaid i ti newid dy arian. Mae’n bwysig dy fod yn gwybod y gyfradd gyfnewid a'r ffi gomisiwn sy’n rhaid i ti ei thalu er mwyn cael y fargen orau bosib.

Cyllid busnes
Mae mathemateg a chyllid yn chwarae rhan allweddol ym myd busnes. Tybed ai ti fydd yr entrepreneur nesaf i wneud dy filiynau?

Mesuriadau bras - Canolradd ac Uwch
Mae mesuriadau’n hanfodol ar gyfer nifer o grefftau a gyrfaoedd. Os wyt yn deall mai ffigur bras yw pob mesuriad, gallai dy rwystro rhag gwneud unrhyw gamgymeriadau.

Diagramau Venn
Mae diagramau Venn yn adnodd defnyddiol ym myd ystadegau. Unwaith y byddi’n gyfarwydd â’r rhain, byddi’n gallu rhoi trefn ar bob math o grwpiau a setiau.

Algebra
Graffiau
Gallwn ddefnyddio graffiau er mwyn cyflwyno data’n eglur, ac i’n cynorthwyo wrth wneud gwaith cyfrifo, er enghraifft ar ffurf graffiau trawsnewid a graffiau teithio. Gall graffiau fod yn gamarweiniol.
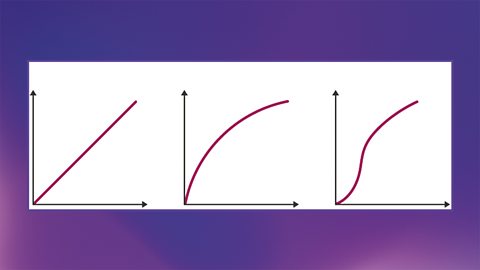
Llunio a defnyddio tangiadau – Uwch yn unig
Mae gallu llunio a defnyddio tangiadau yn sgiliau defnyddiol er mwyn cwblhau gwaith geometrig ar gylchoedd a graddiant cromliniau, yn ogystal â chyfrifo’r arwynebedd o dan graffiau.
πÛ¥⁄¥«∞˘≥ææ±∑…±Ù√¢≥Ð
Rydyn ni’n defnyddio fformiwlâu i gyfrifo pethau fel cyflogau neu gostau. Bydd y costau hyn yn amrywio yn ôl ffactorau megis nifer yr oriau a weithiwyd neu nifer y dyddiau llog sydd eu hangen.

Geometreg a Mesur
Loci a gwneud lluniadau
I wneud lluniadau, bydd angen pensil, pren mesur a phâr o gwmpasau. Defnyddir loci i ganfod ardaloedd sy’n bodloni meini prawf megis pellter penodol oddi wrth bwynt neu hanner ffordd rhwng dwy linell.
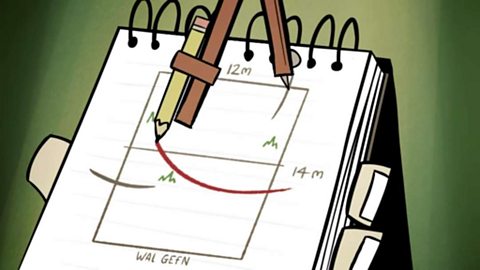
Theorem Pythagoras – Canolradd ac Uwch
Mae theorem Pythagoras yn caniatáu i ni gyfrifo hydoedd mewn trionglau ongl sgwâr. Gwelir trionglau ongl sgwâr mewn bywyd bob dydd – o ddimensiynau teledu i ysgol sy'n gorffwys yn erbyn wal.

Trigonometreg – Canolradd ac Uwch
Mae perthnasau trigonometrig yn bwysig iawn yn y diwydiant adeiladu a chynllunio ac yn caniat√°u cyfrifo hydoedd ac onglau anhysbys yn drachywir.

Helaethiadau/Siapiau tebyg – Canolradd ac Uwch
Mae ffactorau graddfa’n sicrhau bod siâp yn aros yn yr un cyfraneddau pan fo’r maint yn newid. Gall hyn fod yn bwysig wrth newid maint llun i wneud yn siŵr nad yw’r ddelwedd yn cael ei haflunio.

Mapiau
Mae mapiau a lluniadau wrth raddfa’n ffurfio rhan hanfodol o’n bywyd bob dydd. Mae lluniadau wrth raddfa’n ddefnyddiol mewn gyrfaoedd megis pensaernïaeth. Rhaid i ni ddeall cyfeiriannau hefyd.

Trawsnewid rhwng unedau metrig ac imperial
Oherwydd bod cydweithrediad rhyngwladol mor bwysig i ddiwydiant a'r economi, mae'n hanfodol gallu trosi rhwng unedau metrig ac imperial.

Dadansoddi dimensiynol - Canolradd ac Uwch
Mae dadansoddi dimensiynol yn caniat√°u i ni dynnu casgliadau yngl≈∑n √¢ fformiwl√¢u. Mae'n darparu ffordd amgen i ni o wirio ein cyfrifiadau ein hunain a rhai pobl eraill.

Mesurau cyfansawdd
Mae mesurau cyfansawdd yn fesurau sy’n cynnwys dwy uned wahanol neu fwy, ee m/s, g/cm³, poblogaeth fesul km² a milltiroedd y galwyn. Rydyn ni’n gweld mesurau cyfansawdd mewn pob math o gyd-destunau.

Perimedr ac arwynebedd
Gall gwybod sut i ddod o hyd i berimedr neu arwynebedd si√¢p fod yn ddefnyddiol mewn bywyd bob dydd. Defnyddia hyn mewn cyfrifiadau i ddod o hyd i faint o ddeunyddiau sydd eu hangen a'r gost.

Arwynebedd arwyneb a chyfaint
Gallwn gyfrifo cyfaint siapiau 3D er mwyn canfod eu cynhwysedd neu faint o ofod maen nhw’n ei lenwi. Gallwn hefyd ganfod yr arwynebedd arwyneb, sy’n nodi cyfanswm arwynebedd pob un o’u hwynebau.

Ystadegau
Samplu data - Canolradd ac Uwch
Mae samplu yn ein helpu i amcangyfrif nodweddion poblogaeth fawr trwy ddefnyddio gr≈µp cynrychioladol llai. Gall hyn fod yn ddefnyddiol wrth gynnal ymchwil marchnad a phrofion meddygol.

Amlder cronnus - Canolradd ac Uwch
Rydyn ni’n aml yn defnyddio tablau amlder cronnus i ddangos setiau mawr o ddata di-dor neu ddata arwahanol. Mae histogramau yn cael eu defnyddio i ddangos data pan fo maint dosbarthiadau yn wahanol.

Cyfartaleddau ac amrediad
Mae cyfartaleddau’n rhoi gwybodaeth i ni am set o ddata rhifiadol, yn rhoi gorolwg o’r gwerthoedd a dweud wrthyn ni beth yw’r canlyniad mwyaf cyffredin. Mae’r amrediad yn fesur o wasgariad y data.

Amrediad a phlotiau blwch a blewyn
Mae plotiau blwch a blewyn yn ffordd effeithiol o gymharu dosraniadau a chrynhoi eu nodweddion yn hawdd. Defnyddir y diagramau hyn yn aml wrth ddadansoddi data ac mewn gwaith ystadegol.

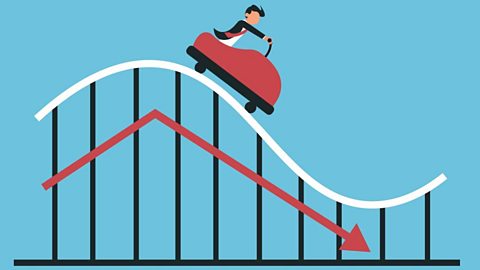
Trafod canlyniadau
Mae cynrychioliadau graffigol o ddata yn gyffredin yng nghymdeithas heddiw. Mae deall a dehongli graffiau yn gywir yn sgil hanfodol bwysig sy'n ddefnyddiol ym meysydd gwahanol o fywyd.
Links
- External linkExternal link
- External linkExternal link
- SubscriptionSubscription