Rhif
Ffactorau cysefin
Mae ffactorau cysefin, lluosrifau cyffredin lleiaf a ffactorau cyffredin mwyaf yn ein galluogi i ddatrys problemau bywyd bob dydd. Mae hwn yn faes diddorol fydd yn gymorth i ddeall rhifau’n well.
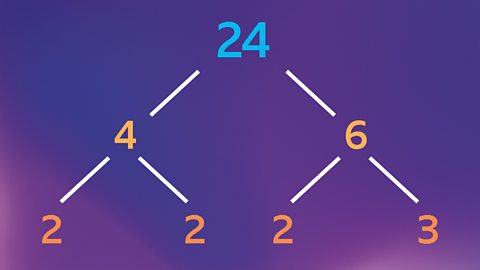
±∑¥«ªÂæ±≤π≤‘≥ŸÃ˝æ±≤‘ªÂ±≥¶≤ı
Mae indecsau’n ffordd o gynrychioli rhifau a llythrennau sydd wedi eu lluosi â’u hunain nifer o weithiau. Maen nhw’n ei gwneud yn haws i ni ddatrys problemau sy’n cynnwys pwerau.

Diagramau Venn
Mae diagramau Venn yn adnodd defnyddiol ym myd ystadegau. Unwaith y byddi’n gyfarwydd â’r rhain, byddi’n gallu rhoi trefn ar bob math o grwpiau a setiau.

πÛ¥⁄≥Ð∞˘¥⁄Ã˝≤ı≤π¥⁄¥«≤‘¥«±Ù
Mae gwneud cyfrifiadau gyda rhifau mawr neu fach iawn yn anodd. Mae’n haws ymdrin â chyfrifiadau o’r fath, fel rhai sy’n ymwneud â’r gofod, drwy drawsnewid rhifau i mewn ac allan o ffurf safonol.

Cymhareb
Mae cymhareb yn dangos y berthynas rhwng dau werth. Gallan nhw fod mewn cyfrannedd union ac un yn cynyddu wrth i'r llall gynyddu, neu mewn cyfrannedd gwrthdro; mae un yn cynyddu wrth i'r llall leihau.

Mesuriadau bras - Canolradd ac Uwch
Mae brasamcanu’n cynnwys amcangyfrif, talgrynnu i bwerau o 10, llefoedd degol a ffigurau ystyrlon.

Termau mathemategol
Mae deall termau mathemategol yn gam pwysig tuag at ddealltwriaeth well o’r pwnc. Dysga ystyr wedi ei sgwario, rhif ciwb, ail isradd, trydydd isradd a chilydd, a sut i’w defnyddio.

Algebra
Hafaliadau llinellau
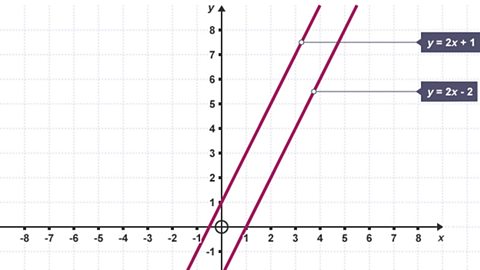
Edrycha sut i blotio ym mhedwar pedrant graff a sut i lunio llinellau syth. Gallwn gasglu gwybodaeth am raddiant a safle’r llinellau, er enghraifft, a ydyn nhw’n baralel neu berpendicwlar ai peidio.
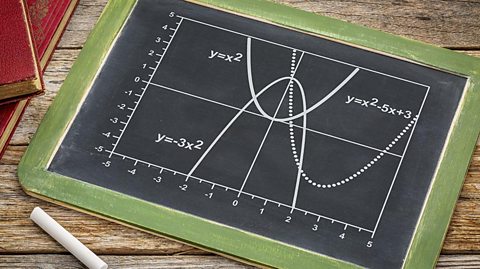
Hafaliadau cromliniau - Canolradd ac Uwch
Mae graffiau cwadratig, ciwbig ac esbonyddol yn dri gwahanol fath o graffiau crwm. Gallwn eu defnyddio i ddatrys hafaliadau sy’n gysylltiedig â’r graff.
Algebra sylfaenol
Mae algebra’n ddefnyddiol iawn yn ein byd modern lle mae mathemateg yn cael ei ddefnyddio’n eang iawn. Mae hyn yn cynnwys ehangu cromfachau, casglu termau ac amnewid mewn fformiwlâu.
Hafaliadau a fformiwl√¢u
Dysga sut i ddatrys, ffurfio a thrin mynegiadau algebraidd gan gynnwys symleiddio ac ad-drefnu hafaliadau. Dysga sut i ddatrys drwy ddefnyddio dull profi a gwella.
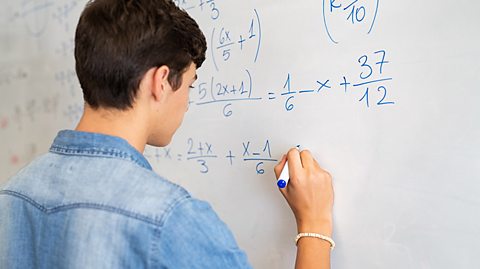
Ffactorio - Canolradd ac Uwch
Mae ffactorio’n ffordd o ysgrifennu mynegiad fel lluoswm o’i ffactorau gan ddefnyddio cromfachau. Rydyn ni’n gwneud hyn drwy gael gwared ag unrhyw ffactorau sy’n gyffredin i bob term yn y mynegiad.

Mynegiadau cwadratig - Canolradd ac Uwch
Defnyddir hafaliadau cwadratig yn aml yn algebra, er enghraifft wrth ddisgrifio mudiant taflegryn. Dysga sut i ffurfio a thrin hafaliadau cwadratig a sut i’w datrys gydag amryw o ddulliau gwahanol.

Dilyniannau
Gall dilyniannau fod yn llinol, yn gwadratig neu’n ymarferol ac wedi eu seilio ar fywyd bob dydd. Gallwn ni ganfod termau mewn dilyniannau yn gyflymach trwy ganfod rheolau cyffredinol.

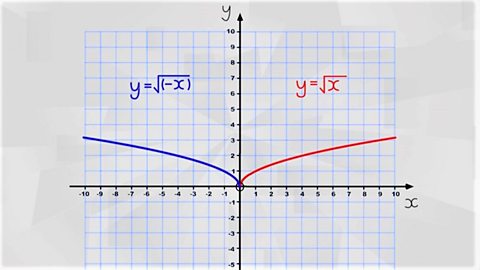
Ffwythiannau - Uwch yn unig
Gallwn drawsffurfio ffwythiannau graffiau i ddangos symudiadau ac adlewyrchiadau. Mae dylunwyr graffeg a modelwyr 3D yn defnyddio trawsffurfiadau graffiau i ddylunio gwrthrychau a delweddau.
Anhafaleddau - Canolradd ac Uwch
Algebra yw un o’r arfau mwyaf pwerus ym myd mathemateg – hebddo, ni fyddai gennyn ni dechnoleg gyfrifadurol fodern, datblygiadau meddygol na theithiau awyren fel y gwyddwn ni amdanyn nhw heddiw.

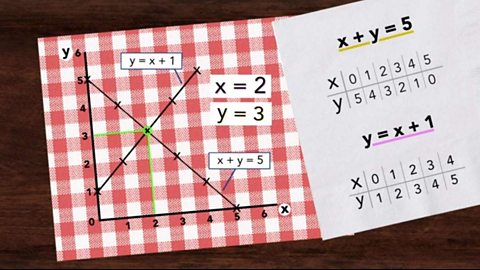
Hafaliadau¬Ýcydamserol - Canolradd ac Uwch
Mae angen defnyddio sgiliau algebraidd wrth ymdrin â hafaliadau cydamserol er mwyn canfod gwerth yr anhysbysion mewn dau hafaliad neu fwy, sy’n wir ar yr un pryd.
Geometreg a Mesur
Sector, segment ac arc - Uwch yn unig
Weithiau mae angen i ni wybod sut i gyfrifo gwerthoedd ar gyfer rhannau penodol o’r cylch. Gall y rhain gynnwys hyd arc, arwynebedd a pherimedr sector ac arwynebedd segment.

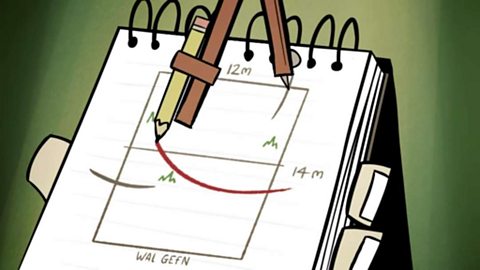
Loci a gwneud lluniadau
I wneud lluniadau, bydd angen pensil, pren mesur a phâr o gwmpasau. Defnyddir loci i ganfod ardaloedd sy’n bodloni meini prawf megis pellter penodol oddi wrth bwynt neu hanner ffordd rhwng dwy linell.
Polygonau
Mae siapiau, geometreg ac onglau’n feysydd pwysig ym myd mathemateg. Cyfrifa’r onglau mewn polygonau rheolaidd ac afreolaidd a cher ati i greu brithweithiau a phatrymau teils.

Cylchoedd - Canolradd ac Uwch
Siapiau 2D gydag un ochr a dim corneli yw cylchoedd. Mae’r cylchyn bob amser yr un pellter o’r canol – y radiws. Rhannau gwahanol o’r cylch yw sector, segment, arc a chord.

Trawsffurfiadau
Mae trawsffurfiad yn newid maint neu safle siâp. Mae siâp tebyg yn amrywio o ran ei faint. Mae siapiau cyfath yn union yr un fath. Mae ffactorau graddfa’n cyfrifo arwynebedd a chyfaint siapiau cyfath.

Ystadegau
Histogramau - Uwch yn unig
Mae histogramau’n ffordd o gynrychioli data. Maen nhw’n debyg i siartiau bar, ond yn dangos y dwysedd amlder yn hytrach na’r amlder. Gallwn eu defnyddio i ganfod gwybodaeth am ddosraniad y data.
Tebygolrwydd
Mathemateg siawns a lwc yw tebygolrwydd. Fe'i ddefnyddir mewn sawl cyd-destun yn y byd go iawn, fel peirianneg, meddygaeth a mwy. Dysga sut i gyfrifo a deall tebygolrwydd mewn amryw o sefyllfaoedd.

Tebygolrwydd pellach - Canolradd ac Uwch
Mae deall tebygolrwydd yn hanfodol mewn nifer o ddiwydiannau, megis y proffesiwn meddygol a’r byd ariannol. Dysga am y rheolau AC/NEU, diagramau cangen a samplu heb amnewid.

Links
- External linkExternal link
- External linkExternal link
- SubscriptionSubscription