Axes
All graphs have an \({x}\)-axis and a \({y}\)-axis.
Here is a diagram of a typical set of axes.
The point \({(0,~0)}\) is called the origin.
The horizontal axis is the \({x}\)-axis.
The vertical axis is the \({y}\)-axis.
Key point
The x-axis is horizontal, and the y-axis is vertical.
One way to remember which axis is which is 'x is a cross so the \({x}\)-axis is across'.
Or you can remember’ y is up’ or ‘wise up’.
Coordinates
Coordinates are written as two numbers, separated by a comma and contained within round brackets.
For example, \({(2,~3)}\), \({(5,~7)}\) and \({(4,~4)}\).
The first number refers to the \({x}\)-coordinate.
The second number refers to the \({y}\)-coordinate.
Coordinates are written alphabetically - so x comes before y (x, y).
One way to remember is 'you go along the hallway before you go up the stairs'.
Plotting coordinates
When describing coordinates, always count from the origin.
For example, to to describe the position of point A in the following diagram, start at the origin and move two squares in the horizontal (\({x}\)) direction.
Then move three squares in the vertical (\({y}\)) direction.
The coordinates of point A are therefore \({(2,~3)}\).
Similarly, the coordinates of point B are \({(8,~9)}\).
The four quadrants
Remember the rule still applies for four quadrants: 'you always go along the hallway before you go up or down the stairs'.
Extending the \({x}\) and \({y}\) axes beyond the origin reveals the negative scales.
The regions separated by the axes are called quadrants.
There are four quadrants in total.
Coordinates in these quadrants are still described in terms of \({x}\) and \({y}\), but now the values of both \({x}\) and \({y}\) can be either positive or negative.
For example in the diagram opposite:
*The coordinates of A are \({(-2,~3)}\)*The coordinates of B are \({(-3,~-4)}\)
Question
What are the coordinates of C for each of these examples?
What are the coordinates of C for each of these examples?
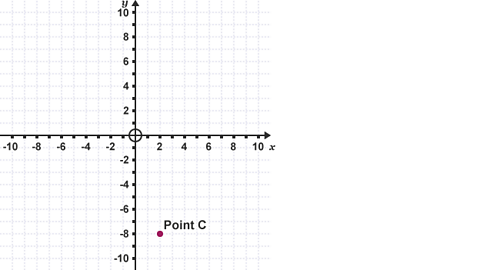
Image caption, What is the coordinate of point C?
Image caption, Point C (2, -8)
Image caption, What is the coordinate of point C?
Image caption, Point C (-9, 4)
Image caption, What is the coordinate of point C?
Image caption, Point C (-6, -4)
Image caption, What is the coordinate of point C?
Image caption, Point C (1, -6)
Image caption, What is the coordinate of point C?
Image caption, Point C (3, -4)
1 of 10
Test yourself
Question 1
To reach point \({A}\) from the origin you have to move \({4}\) squares to the right and \({7}\) squares up.
What are the coordinates of \({A}\)?
a) \({(4,~7)}\)
b) \({4,~7}\)
c) \({(7,~4)}\)
Answer
To reach \({A}\) from the origin \({(0,~0)}\) you have to move \({4}\) squares across, then \({7}\) squares up.
So, the coordinates of \({A}\) are: \({(4,~7)}\).
Question 2
What are the coordinates of this point?
Answer
\((2, 6)\)
Question 3
To reach point \({B}\) from the origin you have to move \({4}\) squares to the left and \({2}\) squares down.
What are the coordinates of \({B}\)?
Answer
You have to move across first \({(-4)}\) and then down \({(-2)}\)
So the correct answer is \({(-4,~-2)}\).
Question 4
To reach the origin from point \({A}\), you have to move \({2}\) squares down and \({3}\) squares to the right.
What are the coordinates of \({A}\)?
Answer
You have to think backwards here and go from the origin to \({A}\).
Also, remember to move across first.
So, the correct answer is \({(-3,~2)}\).
Question 5
What are the coordinates of this point?
Answer
\({(-4,2)}\)
Question 6
What are the coordinates of this point?
Answer
\({(0, -6)}\).
Question 7
What are the coordinates of this point?
Answer
\({(5, -4)}\).
Question 8
\({PQRS}\) is a square.
Given \({P~(3,~4)}\), \({Q~(3,~-1)}\), and \({R~(8,~-1)}\), what are the coordinates of \({S}\)?
You can draw this out on squared paper to help you.
Answer
You could draw this on graph paper to see that the length of the side of the square is \({5}\).
This will help you get the correct answer which is: \({(8,~4)}\).
Question 9
\({ABCD}\) is a rectangle.
Given that \({A}\) is \({(2,~5)}\), \({B}\) is \({(2,~-3)}\) and \({C}\) is \({(-4,~-3)}\), what are the coordinates of \({D}\)?
You can draw this out on squared paper to help you.
Answer
The correct answer is: \({(-4,~5)}\).
You need to move \({8}\) squares up from \({C}\), or \({6}\) squares to the left of \({A}\).
Question 10
If you plot these points, you would notice that they lie on the same straight line: \({(1,~3)}\), \({(2,~6)}\), \({(0,~0)}\).
Which of the following points would also lie also on this line?
a) \( {(3,~9)}\)
b) \({(3,~8)}\)
c) \({(-1,~-4)}\)
Answer
The correct answer is: a) \({(3,~9)}\)
Have you noticed that the \({y}\)-coordinate is always three times the \({x}\)-coordinate for points on this line?
More on Algebra
Find out more by working through a topic
- count17 of 29
- count18 of 29

- count19 of 29

- count20 of 29
