Counting squares
A square centimetre is the area within a square with sides of length \({1~cm}\), as shown here.
We say that it has an area of \({1~cm}^{2}\) (\({1~cm}\) squared).
This rectangle contains six squares.
Each of the squares has an area of \({1~cm}^{2}\), so the area of the rectangle is \({6~cm}^{2}\).
Question
By counting the squares, find the area of the following shapes:
a)
b)
Answer
a) \({10~cm}^{2}\)
b) \({8~cm}^{2}\)
Remember, there are six whole squares and four half squares in the triangle.
Two half squares can be put together to make a whole.
Estimating area
It is not always possible to find the exact area of shapes that don鈥檛 fit exactly onto a grid.
The area can be estimated by counting the squares that are covered halfway or more.
Example
Estimate the area of this leaf.
Mark each square that you have included so that you don鈥檛 count it twice.
The area of this leaf is approximately 21 squares.
Estimate area by counting the squares that are half or more.
Question
Estimate the area of this circle.
(each square has an area of \({1~cm}^2\))
Answer
\(38 cm^2\)
Rectangles
Another way to find the area of a rectangle is to multiply its length by its width.The formula is: \(area = length \times width\)
Question
What is the area of this rectangle?
Answer
\({A}={l}\times{w}\)
\({A}={8~cm}\times{3~cm}\)
\({A}={24~cm}^{2}\)
If you know the area and one of the sides of the rectangle, the other side can be found by rearranging the formula as follows:
\(length = area \div width\)
\(width = area \div length\)
Test section
Question
What is the width of this rectangle?
Answer
\({A}={l}\times{w}\)
\({20}={5}\times{w}\)
\({w}={4~cm}\)
Or using \({width}={area}\div{length}\)
\({w}={20}\div{5}\)
\({w}={4~cm}\)
Question
What is the length of this rectangle?
Answer
The area is \(\text{56 cm}^2\) and the width is \(\text{7 cm}\), so the length is \(56 \div 7 = \text{8 cm}\)
Question 1
Find the area of the following shape by counting squares on the \({cm}\) squared paper provided?
Answer
Count the \({1}~{cm}^{2}\) squares to get an answer of \({12}~{cm}^{2}\)
Question 2
What is the area of a rectangle that is \({6}~{cm}\) long and \({5}~{cm}\) wide?
Answer
The formula to find the area of a rectangle is \({area}={length}\times{width}\).
Therefore \({5}~{cm}\times{6}~{cm}={30}~{cm}^{2}\).
Question 3
The area of a rectangle is \({24}~{cm}^{2}\).
If the length of the rectangle is \({8}~{cm}\), what is the width?
Answer
Rearrange the formula to get \({width}={area~of~rectangle}\div{length}\).
In this case \({24}~{cm}^{2}\div{8}~{cm}={3}~{cm}\).
Question 4
Estimate the area of this shape.
Answer
\(12\) squares
Question 5
Estimate the area of the pond.
(each square has an area of \({1~m}^2\))
Answer
\({11~m}^2\)
Question 6
What would be the best estimate for the area of this leaf? (each square has an area of \({1~m}^2\))
Answer
\({41~cm}^2\)
Question 7
Estimate the area of the island.
(each square has an area of \({5~km}^2\))
Answer
\({100~km}^2\)
Triangles
Look at this triangle.
The base of the triangle is the width of the rectangle and the perpendicular height of the triangle is equal to the height of the rectangle.
If you multiply the base by the perpendicular height, you get the area of a rectangle.
The area of the triangle is half the area of the rectangle.
So, to find the area of a triangle, multiply the base by the perpendicular height and divide by two. The formula is:
\(Area = \frac{(b \times h)}{2}\)
Remember \({h}\) stands for the perpendicular height of the triangle.
Question
Find the area of this triangle:
Answer
The area of the triangle is:
\(A=\frac{({b}\times{h})}{2}\)
\(=\frac{(5\times8)}{2}=\frac{40}{2}\)
\(={20~cm}^2\)
Compound shapes
There are two different methods for finding the area of a compound shape.
Method 1
Divide the shape into squares and rectangles, find their individual areas and then add them together.
The length of the larger rectangle is \(4 + 4 + 4 = 12~cm\)
\(Area = 16 + 16 + 48 = {80~cm}^{2}\)
Method 2
Imagine the shape as a large rectangle with a section cut out.
The length of the outer rectangle is \(4 + 4 + 4 = 12~cm\)
Find the area of the large rectangle (\(12 \times 8\)) and then subtract the part that has been cut out (\(4 \times 4\))
\(Area = (12 \times 8) - (4 \times 4) = 96 - 16 = \text{80 cm}^2\)
Parallelograms
The area of a parallelogram is the \(base \times perpendicular~height~(b \times h)\).
Rearranging a parallelogram
You can see that this is true by rearranging the parallelogram to make a rectangle.
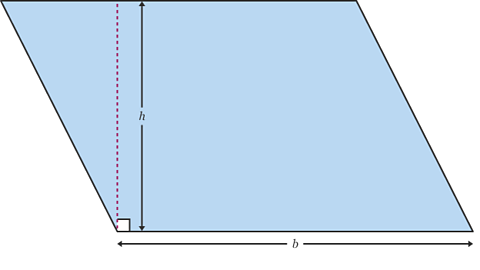
Image caption, Regular parallelogram showing base and height.
1 of 3
Use the perpendicular height of the parallelogram, not the sloping height.
Question
Find the area of this parallelogram:
Answer
The area is \({7~cm}\times{3~cm}={21~cm}^{2}\).
Remember to use the perpendicular height of the parallelogram.
Parallelograms - base or height
You now know how to find the area of a parallelogram, but what happens if you need to find the base or the height?
You just have to rearrange the formula.
\(A = b \times h\)
\(h={A}\div{b}\) or \(h=\frac{A}{b}\)
\(b={A}\div{h}\) or \(b=\frac{A}{h}\)
Question
The area of this parallelogram is \(\text{12 cm}^2\).
What is its perpendicular height?
Answer
\(h = A \div b\)
\(h = 12 \div 4 = 3~cm\)
Question
Find the length of the base of this parallelogram:
Answer
\(b = A \div h\)
\(b = 40 \div 5 = 8~cm\)
Remember to divide the area by the perpendicular height.
Area of a trapezium
The area of a trapezium is given by \({A}=\frac{(a+b)}{2}\times{h}\).
You can see that this is true by taking two identical trapezia (or trapeziums) to make a parallelogram.
Area of a trapezium
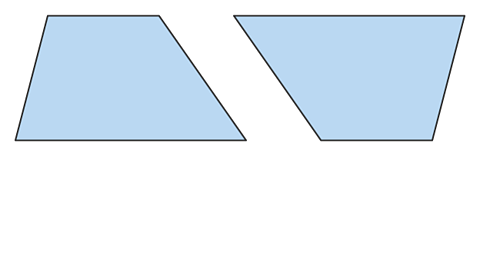
Image caption, Turn one trapezium through 180掳.
1 of 4
For a parallelogram, the area is \({A}={b}\times{h}\)
So, area of \({2}\) trapeziums \(= {(a + b)} \times {h}\)
Area of \({1}\) trapezium \(= \frac{1}{2} \times {(a + b)} \times {h}\)
This becomes, for a trapezium, \({A}=\frac{(a+b)}{2}\times{h}\)
Use the perpendicular height of the trapezium, not the sloping height.
Question
Find the area of this trapezium:
Answer
The area is \({A}=\frac{(4+10)}{2}\times{6}\)
\(={42~cm}^{2}\)
Remember to use the perpendicular height of the trapezium.
Test section
Question 1
What is the area of a triangle if the base is \({10}~{m}\), and the height is \({4}~{m}\)?
Answer
The area of a triangle \(={({base}\times{height})}\div{2}\), \({({10}~{m}\times{4}~{m})}\div{2}={20}~{m}^{2}\).
Question 2
The area of a triangle is \({45}~{cm}^{2}\).
If the height of the triangle is \({9}~{cm}\) what is the length of its base?
Answer
Rearrange the formula like this: \({base}={({area~of~triangle}\times{2})}\div{height}\). In this case \(({45}~{cm}^{2}\times{2})\div{9}~{cm}={10}~{cm}\).
Question 3
What is the area of the following compound shape?
Answer
To calculate the area of a compound shape, you need to calculate the area of the square and triangle separately before adding the two together, like this: \(({4}~{cm}\times{4}~{cm})+(({4}~{cm}\times{2}~{cm})\div{2})={20}~{cm}^{2}\).
Question 4
What is the area of the following compound shape?
Answer
To calculate the area of a compound shape you could calculate the area of the big rectangle and then subtract the area of the square: \(({12}~{cm}\times{8}~{cm})-({4}~{cm}\times{4}~{cm})={80}~{cm}^{2}\).
Question 5
What is the area of the following parallelogram?
Answer
The formula for the area of a parallelogram is \({base}\times{height}\), namely \({9}~{cm}\times{6}~{cm}={54}~{cm}^{2}\) in this instance.
Question 6
What is the height of a parallelogram if its area is \({21}~{cm}^{2}\) and its base is \({7}~{cm}\)?
Answer
Rearrange the formula like this: \({height}={area~of~parallelogram}\div{base}\).
Therefore: \({21}~{cm}^{2}\div{7}~{cm}={3}~{cm}\).
Question 7
What is the area of the following trapezium?
Answer
The formula for the area of a trapezium is \(\frac{1}{2}({a}+{b})\times{h}\).
In this instance, \(\frac{1}{2}({14}+{8})\times{6}={66}~{cm}^{2}\).
More on Shape, space and measures
Find out more by working through a topic
- count10 of 52
