Problem 7 - Traffic calming
Problem 7 is all about calculating the average speed of a journey.
Maths teacher Chris Smith and pupils from Grange Academy are here to explain.
The Maths Week Scotland Daily Challenges have been set by the Scottish Mathematical Council.
CHRIS: This challenge is all about calculating speed. But listen carefully, it's a bit of a trick question.
With the new twenty miles per hour zones now in place, Rivka's journey to work takes longer than it used to. Now she can drive only half the distance at thirty miles per hour. While the other half is at the reduced speed limit of twenty miles per hour.
What is Rivka's average speed over the whole journey to work?
Explain your answer.
How far does is the journey? Do we know that? We don't have that. Yeah?
PUPIL: The answer isn't as easy as it first seems.
CHRIS: Half of the journey going at thirty, half the journey going at twenty, right, okay.
PUPIL: It helps to know that speed equals distance divided by time.
PUPIL: We don't know how long the journey takes or how far it is so you might have to invent a value.
CHRIS: So we don't know the overall distance but we know that something happens halfway.
PUPIL: Good luck and try your best.
So here's the challenge:
With the new 20 zones now in place, Rivka’s journey to work takes longer than it used to.
- Rivka can drive half the distance at 30 mph
- while the other half is at the reduced speed limit
What is Rivka’s average speed over the whole journey to work and back home?

Need a hint?
- The answer isn’t as easy as it first seems
- It helps to know that speed = distance Г· time
- We don’t know how long the journey takes or how far it is, so you might have to invent a value
Solution
Worked out the answer? Here's how you can do it.
In this challenge, we had to calculate the average speed of Rivka's journey.
Did you work it out?
This problem is sometimes considered a trick question,. The obvious answer of adding thirty and twenty together and then dividing by two to get twenty five miles per hour is actually wrong.
The first thing we have to consider is the formula we use to calculate speed. The average speed is equal to the total distance divided by the total time of the journey.
This problem can only be solved by using the distance between Rivka's home and her workplace and calculating the time taken for the parts of the journey travelled at thirty miles per hour and the parts of the journey travelled at twenty miles per hour separately and then combining them together. That distance is not stated and yet strangely it doesn't affect the answer.
Since any distance will do, let's say it's exactly twenty miles between Rivka's home and her work so that she does ten miles at thirty miles per hour and ten miles at twenty miles per hour. The time taken to travel ten miles at thirty miles per hour is one third of an hour, which is twenty minutes, the time taken to travel ten miles at twenty miles per hour is half an hour, which is thirty minutes.
So overall Rivka has travelled twenty miles in fifty minutes, which is the same average speed as four miles in ten minutes or twenty four miles per hour.
So two hundred and forty divided by ten gives you twenty four miles per hour.
Lovely, Anna, that's good.
If you're not convinced that the answer is the same regardless of the distance Rivka drives, try some other distances to her workplace.
Such as six miles or ten miles.
This was a tough problem to solve. Did you figure it out?
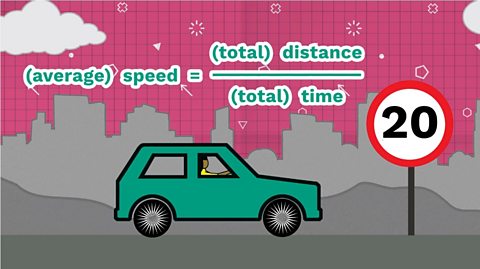
The first thing we have to consider is the formula we use to calculate speed:
speed = distance Г· time
We can only solve this problem by using the distance between Rivka’s home and work to calculate the time taken for the two parts of the journey.
We don’t know the distance but we can make one up. This won’t affect the answer because it won’t affect the proportion of the journey travelled at each speed.


Let's say it's exactly 20 miles between Rivka's home and work.
So she drives 10 miles at 30 miles per hour and 10 miles at 20 miles per hour.
- \(10 \text{ miles at }30 \text{ miles per hour } = \frac{1}{3} \text{ of an hour } = 20 \text{ minutes }\)
- \(10 \text{ miles at } 20 \text{ miles per hour } = \frac{1}{2} \text{ of an hour } = 30 \text{ minutes }\)


Overall, Rivka travels \(20 \text{ miles in } 50 \text{ minutes}\)
Simplify by dividing by \(5\):
\(= 4 \text{ miles in } 10 \text{ minutes}\)
Multiply by \(6\) to find the speed in miles per hour:
\(= 24 \text{ miles per hour }\)
So the average speed for Rivka’s journey is 24 miles per hour.

Maths Week Scotland 2023. listMaths Week Scotland 2023
Try out all the daily challenges from Maths Week Scotland 2023.

Maths Week Scotland 2022. listMaths Week Scotland 2022
Try out all the daily challenges from Maths Week Scotland 2022.

Maths Week Scotland 2021. listMaths Week Scotland 2021
Want more maths challenges? Here are all the problems from 2021.

More on Problem solving
Find out more by working through a topic
- count8 of 21

- count9 of 21

- count10 of 21
- count11 of 21
