Prime numbers
A prime number has exactly two factors, itself and one.
The first ten prime numbers are \({2}\), \({3}\), \({5}\), \({7}\), \({11}\), \({13}\), \({17}\), \({19}\), \({23}\) and \({29}\).
Key points
The only even prime number is \({2}\). All other even numbers are divisible by \({2}\).
The number \({1}\) is not prime because a prime number has exactly two factors and \({1}\) only has one factor.
Question
What are the prime numbers between \({50}\) and \({60}\)?
Answer
The prime numbers are \({53}\) and \({59}\).
Factors and multiples
Factors
The factors of a number are the numbers that divide into it exactly.
The factors of \({12}\) are \({1}\), \({2}\), \({3}\), \({4}\), \({6}\) and \({12}\).
The factors of \({10}\) are \({1}\), \({2}\), \({5}\) and \({10}\).
The factors of \({11}\) are \({1}\) and \({11}\) (so \({11}\) is a prime number).
Multiples
The multiples of a number are the numbers that belong to that number's times table.
The multiples of \({3}\) are \({3}\), \({6}\), \({9}\), \({12}\), \({15}\) \({…}\)
The multiples of \({11}\) are \({11}\), \({22}\), \({33}\), \({44}\), \({55}\) \({…}\)
Key point
The first multiple of any number is that number itself, for example the first multiple of 3 is 3.
Question
List the first five multiples of \({4}\).
Answer
The first five multiples of \({4}\) are \({4}\), \({8}\), \({12}\), \({16}\) and \({20}\).
Factor pairs
Factors are often given as pairs of numbers, which multiply together to give the original number.
These are called factor pairs.
For example, the factor pairs of \({12}\) are:
- \({1}\) and \({12}\)
- \({2}\) and \({6}\)
- \({3}\) and \({4}\)
A square number will have one factor pair consisting of one factor multiplied by itself. This factor is called the square root of the given number.
The factor pairs of \({16}\) are:
- \({1}\) and \({16}\)
- \({2}\) and \({8}\)
- \({4}\) and \({4}\)
Question
List the factor pairs of \({20}\).
Answer
The factor pairs are:
\({1}\) and \({20}\)
\({2}\) and \({10}\)
\({4}\) and \({5}\)
Factor trees
It is often useful to write a number as the product of its prime factors.
This can be done by listing the factor pairs as successive branches in a factor tree.
The branches continue to expand until all the factors are prime numbers.
The final answer is the product of the prime numbers displayed at the end of these branches.
Note that the number \({1}\) is not used within a factor tree.
Write 24 as the product of its prime factors
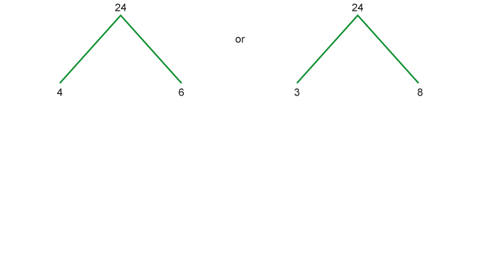
Image caption, You could choose any factor pair to start.
Image caption, Find the factor pair for one of the new factors.
Image caption, Find the remaining factor pairs in the same way.
Image caption, 24 written as the product of its prime factors is 2 √ó 2 √ó 2 √ó 3.
1 of 4
Question
Write \({48}\) as the product of its prime factors.
Answer
\({48}\) written as the product of its prime factors is
\({2}\times{2}\times{2}\times{2}\times{3}\)
Highest common factor (HCF)
The factors of a number are any numbers that divide into it exactly.
The factors of \({12}\) are \({1}\), \({2}\), \({3}\), \({4}\), \({6}\) and \({12}\)
The factors of \({18}\) are \({1}\), \({2}\), \({3}\), \({6}\), \({9}\) and \({18}\)
\({1}\), \({2}\), \({3}\) and \({6}\) are factors of both \({12}\) and \({18}\).
They are known as the common factors of \({12}\) and \({18}\).
So the highest common factor (HCF) of \({12}\) and \({18}\) is \({6}\).
Question
What is the HCF of \({16}\) and \({40}\)?
Answer
The factors of \({16}\) are \({1}\), \({2}\), \({4}\), \({8}\) and \({16}\).
The factors of \({40}\) are \({1}\), \({2}\), \({4}\), \({5}\), \({8}\), \({10}\), \({20}\) and \({40}\).
So the HCF of \({16}\) and \({40}\) is \({8}\).
Lowest common multiple (LCM)
The multiples of a number are all the numbers that it will divide into.
The multiples of \({4}\) are \({4}\), \({8}\), \({12}\), \({16}\), \({20}\), \({24}\), \({28}\), \({32}\), \({36}\), \({40}\), \({44}\) \({…}\)
The multiples of \({6}\) are \({6}\), \({12}\), \({18}\), \({24}\), \({30}\), \({36}\), \({42}\), \({48}\), \({54}\), \({60}\), \({66}\) \({…}\)
\({12}\), \({24}\), and \({36}\) are multiples of both \({4}\) and \({6}\) and are known as the common multiples of \({4}\) and \({6}\).
The lowest number that is a multiple of \({4}\) and \({6}\) is \({12}\).
So the lowest common multiple (LCM) of \({4}\) and \({6}\) is \({12}\).
Question
What is the LCM of \({5}\) and \({8}\)?
Answer
The multiples of \({5}\) are \({5}\), \({10}\), \({15}\), \({20}\), \({25}\), \({30}\), \({35}\), \({40}\) \({…}\)
The multiples of \({8}\) are \({8}\), \({16}\), \({24}\), \({32}\), \({40}\), \({48}\), \({56}\) \({…}\)
So the LCM of \({5}\) and \({8}\) is \({40}\).
Test section
Question 1
List the prime numbers between \({40}\) and \({50}\).
Answer
The prime numbers are \({41},~{43}\) and \({47}\).
All the even numbers are divisible by \({2}\), so not prime.
\({45}\) is divisible by \({5}\) and \({49}\) is divisible by \({7}\), so they are not prime.
Question 2
How many factors does the number \({36}\) have?
Answer
\({36}\) has \({9}\) factors: \({1},~{2},~{3},~{4},~{6},~{9},~{12},~{18}\) and \({36}\).
Question 3
List the first \({4}\) multiples of \({6}\).
Answer
Include \({6}\) along with \({12},~{18}\) and \({24}\).
Question 4
What is the \({5}^{th}\) multiple of \({3}\)?
Answer
The \({5}^{th}\) multiple of \({3}\) is \({15}\).
Question 5
Look at the following list of numbers:
\({2},~{36},~{9},~{8},~{24}\)
Which number is a multiple of \({18}\)?
Answer
\({36}\) is a multiple of \({18}\).
Question 6
Look at the following list of numbers:
\({2},~{36},~{9},~{6},~{24}\)
Which number is a factor of \({18}\), but not a multiple of \({2}\)?
Answer
\({9}\) is a factor of \({18}\), but not a multiple of \({2}\).
Question 7
Write \({36}\) as the product of its prime factors.
Answer
\({2}\times{2}\times{3}\times{3}\).
When you multiply these together you get \({36}\).
Question 8
Find the highest common factor (HCF) of \({32}\) and \({40}\).
Answer
\({8}\) is a common factor of \({32}\) and \({40}\), and is the highest possible value.
Question 9
Find the lowest common multiple (LCM) of \({32}\) and \({40}\).
Answer
The lowest common multiple of \({32}\) and \({40}\) is \({160}\).
Question 10
Find the highest common factor (HCF) of \({48},~{54}\) and \({72}\).
Answer
The highest common factor of \({48}\), \({54}\) and \({72}\) is \({6}\).
More on Prime numbers, factors and multiples
Find out more by working through a topic
- count2 of 5

- count3 of 5

- count5 of 5
