Key points
energyEnergy can be stored and transferred. Energy is a conserved quantity. is stored in many systems in our homes.
Energy can be transferred between energy stores.
Some appliances are more powerful than others so energy can transfer faster.
Common energy stores
There are different stores of energyEnergy can be stored and transferred. Energy is a conserved quantity..
Have a look at this slideshow to explore more about different stores of energy.

Image caption, The kinetic store of an object is filled when an object speeds up, and it empties when an object slows down
Image caption, The gravitational store of an object is filled when an object is raised, and it empties when an object falls or is lowered
Image caption, The elastic store of an object is filled when it is stretched or compressed
Image caption, A chemical store is emptied during a chemical reaction when energy is transferred to the thermal store of the surroundings
Image caption, The thermal store of an object is filled when a substance is heated, and it is emptied when the substance cools down
1 of 5
Common energy transfers in the home
In the home, energyEnergy can be stored and transferred. Energy is a conserved quantity. can be transferred by:
mechanical work – when a force is applied to move an object over a distance
electrical work – when charge flows (electricity)
heating – when there is difference in temperatures
radiation – when energy is transferred as a wave, for example as light or sound.
Common energy stores and transfers in the home

Washing machine
Charges flow in the wires of the motor.
energyEnergy can be stored and transferred. Energy is a conserved quantity. is transferred by doing electrical work to the kinetic energy store of the motor. The motor turns.


Lamp
Charges flow through the filament bulb. Energy is transferred by electrical working to the thermal energy store of the filament bulb. The bulb gets hot.
Energy transfers from the thermal energy store of the bulb by heating and light.


Kettle
Charges flow through the heating element of the kettle. Energy is transferred by electrical working to the thermal energy store of the element. The element gets hot.
Energy transfers from the hot element to the water by heating. The water gets hot.


Gas cooker
Methane gas is a fuel. Energy from its chemical energy store is transferred to the thermal energy store of the flame as it burns.
Energy is transferred by heating and light from the hot flame to the surroundings.

Electrical appliances

If you look at the electrical appliances found in your home you may see labels that show the power rating of the appliance.
powerThe rate of energy transfer. Measured in watts (W). is the amount of energyEnergy can be stored and transferred. Energy is a conserved quantity. transferred each second. Power is measured in watts (W).

If you have a device that has a power rating of 100 watts, this means that 100 jouleThe unit of measurement for energy (J). A kilojoule (kJ) is 1000 joules. of energy are transferred each second.
Some appliances transfer large amounts of energy so their power rating is shown in kilowatts (kW)
1 kilowatt = 1000 watts
1kW = 1000 W
So therefore:
2 kW = 2 x 1000 W
2 kW = 2000 W
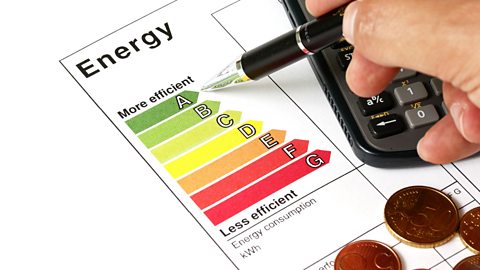
Some appliances are more energy efficient than others. A label shows how energy efficient they are.
Choosing a more energy efficient appliance can reduce energy bills.

Calculating energy transfers
The power rating of an appliance can be used to calculate the amount of energyEnergy can be stored and transferred. Energy is a conserved quantity. transferred whilst it is being used. Apply the following formula to do this:
\(Energy~transferred = Power \times time\)
Energy transferred in joules (J).
Power in watts (W).
Times in seconds (s).
Example
A 800 Watt microwave oven is switched on for 40 seconds. How much energy is transferred to the microwave oven?
\(Energy~transferred = Power \times time\)
\(E =P \times t\)
\(E= 800~W \times 40~s\)
\(E= 32~000~J\)
This answer could also be written as 32 kJ (32 kilojoules).
Converting between hours, minutes and seconds

An appliance is often used for several minutes or hours.
To calculate an energyEnergy can be stored and transferred. Energy is a conserved quantity. transfer value in jouleThe unit of measurement for energy (J). A kilojoule (kJ) is 1000 joules., the time value must be converted into seconds.


There are 60 seconds in a minute. There are 60 minutes in an hour.
Example 1
Convert 5 minutes into seconds.
Remember 1 minute = 60 seconds.
There are 60 seconds per minute. This can be written as 60 seconds/minute.
5 minutes converted to seconds is:
\(5~minutes \times 60~seconds/minute = 300~seconds\)
Example 2
Convert 2 hours into seconds.
Step 1 - convert hours into minutes.
1 hour = 60 minutes.
There are 60 minutes per hour. This can be written as 60 minutes/hour.
2 hours converted to minutes is:
\(2~hours \times 60~minute/hour = 120~minutes\)
Step 2 - convert the minutes into seconds.
1 minute = 60 seconds.
120 minutes converted to seconds is:
\(120~mins \times 60~seconds/minute = 7200~seconds\)
2 hours = 7200 seconds.
Calculating the amount of energy transferred
Example 1
A 2000 watt kettle is turned on for 2 minutes. Calculate the energy transfer to the kettle.
\(Power = 2000~W\)
\( Energy~transferred = ?\)
\(Time = 2~minutes\)
Step 1 - Convert time to seconds:
\(2~minutes \times 60~seconds/minute = 120~seconds\)
Step 2 - Substitute values into equation:
\(Energy~transferred = power \times time\)
\(E = P \times t\)
\(Energy~transferred = 2000~W \times 120~s\)
\(Energy~transferred = 240~000~J\)
If a 2000 W kettle is turned on for 2 minutes, the energy transferred to the kettle is a a total of 240 000 J (240 kJ).
Example 2
A 5 kW oven is turned on for 2 hours. Calculate the energy transfer to the oven.
\(Power = 5~kW\)
\(Energy~transferred = ?\)
\(Time = 2~hours\)
Step 1- convert the power from kW to W:
\(5~kW \times 1000~W/kW = 5000~W\)
Step 2 - convert the time into seconds:
\(2~hours \times 60~minutes/hour = 120~minutes\)
\(120~minutes \times 60~seconds/minute = 7200~seconds\)
Step 3- substitute the values into the equation:
\(Energy~transferred = power \times time\)
\(Energy~transferred = 5000 \times 7200\)
\(Energy~transferred = 36~000~000~J\)
This shows us that 36,000,000 J (36 000kJ) of energy are transferred to a 5 kW oven that is turned on for 2 hours.
Energy bills
Energy companies monitor the amount of energy transferred to our homes using meters.
The companies then use readings from these meters to calculate an electricity or gas bill.


Energy is usually measured in joules (J). One joule of energy is transferred to a one watt device used for one second.
\(Energy~transferred = power \times time\)
\(E = P \times t\)
\(1~J = 1~W \times 1~s\)
However energy companies use a different unit called kilowatt hours (kWh).
Appliances are usually used for long periods of time so very large amounts of energy are transferred.
1 kWh is the amount of energy transferred to a 1kW appliance in 1 hour.
\(Energy~transferred = power \times time\)
\(1~kWh = 1~kW \times 1~h\)
Calculating how much to pay
Energy companies have a set price per kWh or ‘unit’ used. They calculate the energy bill using the following equation:
\(Total~cost = amount~of~energy~used~in~kWh \times cost~per~kWh\)
Example
Gas central heating is used for two weeks. 320 kWh of energy is transferred in.
If 1 kWh costs 5p, calculate the cost of using the central heating.
Total cost = ?
Energy used = 320 kWh
Cost per kWh = 5p
Total cost = amount of energy used in kWh x cost per kWh
Total cost = 320 kWh x 5 p / kWh
Total cost = 1 600 p (or £16).
Click to have a look at a further example.
A 3 kW water heater is used for 2 hours.
If 1 kWh costs 16p, calculate the total cost of using the water heater.
Power = 3kW
Cost per kWh = 16 p
Total cost = ?
This is a two step problem.
Step 1 - calculate the energy transferred.
\(Energy~transferred = power \times time\)
\(E = P \times t\)
\(E = 3~kW \times 2~h\)
\(E = 6~kWh\)
Step 2 - Calculate the cost.
\(Total~cost = amount~of~energy~used \times cost~per~kWh\)
\(Total~cost = 6~kWh \times 16~p/kWh\)
\(Total~cost = 96~p\)
Test your knowledge
Quiz
Play the Atomic Labs game! gamePlay the Atomic Labs game!
Try out practical experiments in this KS3 science game.

More on Energy
Find out more by working through a topic
- count2 of 6

- count3 of 6

- count4 of 6
- count5 of 6
