Exam practice
GCSE maths: Exam-style quiz by topic
Try this quiz based on GCSE Maths past papers. Choose the topic you would like to revise and answer the questions.

GCSE Maths: exam-style questions
Free interactive maths quizzes based on OCR foundation and higher past papers to help you prepare for your GCSE exams, covering common errors in algebra, graphs.

GCSE Maths: quick-fire questions
Prepare for your OCR GCSE maths higher or foundation exam with this free interactive quiz covering topics including fractions, equations and algebra.

Quizzes
Quiz: Whole numbers
This interactive quiz is suitable for GCSE maths students studying writing whole numbers as words, ordering whole numbers, and multiplying and dividing whole numbers.

Quiz: Whole numbers 2
This interactive quiz is suitable for GCSE maths students studying order of operations, negative numbers, adding and subtracting negative numbers.

Quiz: Approximation
This interactive quiz is suitable for GCSE maths students studying approximation, rounding to decimal places, rounding to significant figures, truncation, estimating calculations.

Quiz: Decimals
This interactive quiz is suitable for GCSE maths students studying place value and ordering decimals, adding, subtracting, multiplying and dividing decimals.
Quiz: Multiples and factors
This interactive quiz is suitable for GCSE maths students studying multiples and factors, prime, square and cube numbers, powers and roots, and highest common factor.

Quiz: Laws of indices
This interactive quiz is suitable for GCSE maths students studying using an index or power, law of indices – multiplication and division, and raising a power to a power.
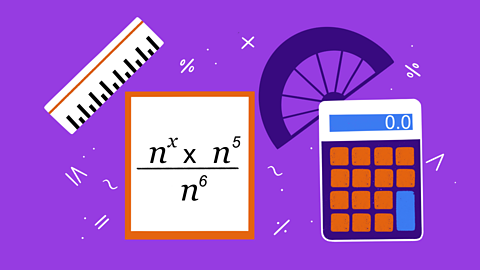
Quiz: Converting between fractions, decimals and percentages
This interactive quiz is suitable for GCSE maths students studying converting decimals to fractions and percentages, fractions to decimals, and percentages to decimals.

Quiz: Fractions
This interactive quiz is suitable for GCSE maths students studying ordering fractions, using fractions, mixed numbers and improper fractions and fraction arithmetic.
Quiz: Fractions 2
This interactive quiz is suitable for GCSE maths students studying ordering and using fractions, multiplying and dividing fractions, fraction arithmetic, and fractions of amounts.
Quiz: Standard form
This interactive quiz is suitable for GCSE maths students studying standard form, converting from standard form, ordering numbers in standard form, and calculating standard form.
Quiz: Surds
This interactive quiz is suitable for GCSE maths students studying simplifying surds, adding and subtracting surds and rationalising denominators.

Quiz: Financial mathematics
This interactive quiz is suitable for GCSE maths students studying wages and salaries, salary and pay, profit and loss, bank statements and savings and VAT.
Quiz: Algebraic expressions
This interactive quiz is suitable for GCSE maths students studying expressions, simplifying expressions, expanding brackets, expanding double brackets and expanding three brackets.
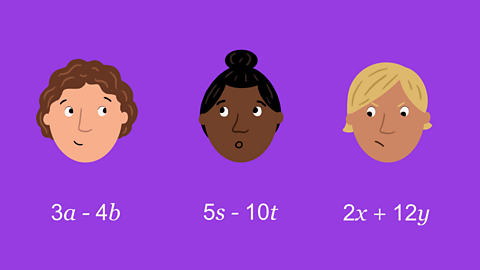
Quiz: Algebraic expressions 2
This interactive quiz is suitable for GCSE maths students studying factorising, using algebra to demonstrate an argument, and proof.
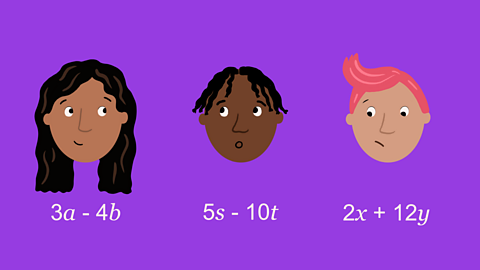
Quiz: Algebraic formulae
This interactive quiz is suitable for GCSE maths students studying formulae, substitution, creating formulae, changing the subject of a formula, rearranging formulae.
Quiz: Solving linear equations
This interactive quiz is suitable for GCSE maths students studying equations and identities, number machines, and solving equations.
Quiz: Solving simultaneous equations
This interactive quiz is suitable for GCSE maths students studying simultaneous equations, and solving simultaneous examples with no common coefficients.

Quiz: Inequalities
This interactive quiz is suitable for GCSE maths students studying inequalities, solving inequalities, integer solutions to inequalities and graphs of inequalities.

Quiz: Straight line graphs
This interactive quiz is suitable for GCSE maths students studying coordinates, straight line graphs, parallel and perpendicular lines and equations of a line through two points.

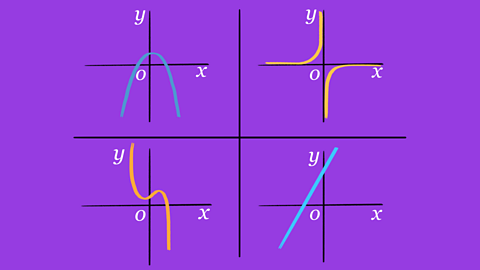
Quiz: Other graphs
This interactive quiz is suitable for GCSE maths students studying quadratic graphs, cubic graphs, reciprocal graphs, exponential graphs.
Quiz: Transformation of curves – Higher
This interactive quiz is suitable for GCSE maths students studying translating graphs and reflections of graphs.
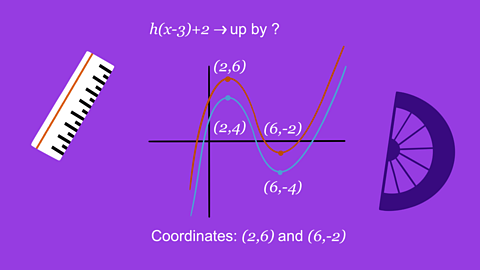
Quiz: Algebraic fractions
This interactive quiz is suitable for GCSE maths students studying simplifying rational expressions, factorising, and adding and subtracting rational expressions.

Quiz: Using and interpreting graphs
This interactive quiz is suitable for GCSE maths students studying real-life graphs, distance-time and displacement-time graphs, speed-time and velocity-time graphs.

Number
Whole numbers - OCR
Numbers can be written in words. Both positive and negative numbers can be added, subtracted, multiplied and divided using rules. These rules must be applied in a specific order.

Approximation - OCR
Approximation includes estimation, rounding to powers of 10, decimal places and significant figures.

Decimals - OCR
Decimals are used every day, for example, when using money. Knowing how to use decimal points and places when adding, subtracting, dividing and multiplying is an important mathematical skill.

Multiples, factors, powers and roots - OCR
Prime numbers, factors and multiples are essential building blocks for a lot of number work. Knowledge of how to use these numbers will improve arithmetic and make calculations more efficient.

Standard form - OCR
Calculations with very big or small numbers can be made easier by converting numbers in and out of standard form.

Laws of indices - OCR
An index, or power, is the small floating number that appears after a number or letter. Indices show how many times a number or letter has been multiplied by itself.

Fractions - OCR
Fractions are used commonly in everyday life, eg sale prices at 1/3 off, or recipes using 1/2 a tablespoon of an ingredient. Knowing how to use fractions is an important mathematical skill.

Converting between fractions, decimals and percentages - OCR
Fractions, decimals and percentages are frequently used in everyday life. Knowing how to convert between them improves general number work and problem solving skills.

Surds - Higher - OCR
Surds are numbers left in square root form that are used when detailed accuracy is required in a calculation. They are numbers which, when written in decimal form, would go on forever.

Financial mathematics - OCR
Financial maths is needed for all jobs, from calculating wages to working out profit, loss and VAT. Knowledge of financial maths is also required to be able to understand bank statements and savings.

Algebra
Algebraic expressions - OCR
Letters can be used to stand for unknown values or values that can change. Formulas can be written and equations solved to solve a range of problems in science and engineering.
Algebraic formulae - OCR
Formulae are used in everyday life, from working out areas and volumes of shapes to converting units of measurement. Knowing how to use and rearrange formulae are very useful skills.

Algebraic fractions - OCR
Algebraic expressions in fraction form are rational. Methods of adding, subtracting, multiplying and dividing fractions plus expanding and factorising can be used to simplify rational expressions.
Solving linear equations - OCR
Forming, using and solving equations are skills needed in many different situations. From balancing accounts to making sense of a mobile phone bill, solving equations is a vital skill.
Solving simultaneous equations - OCR
Simultaneous equations require algebraic skills to find the values of letters within two or more equations. They are called simultaneous equations because the equations are solved at the same time.
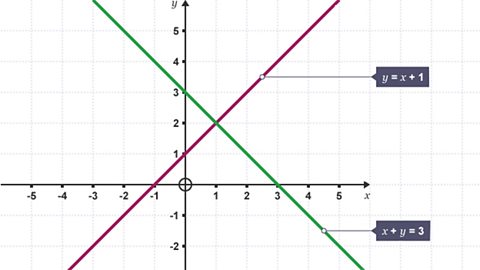
Inequalities - OCR
Inequalities show the relationship between two expressions that are not equal to one another. Inequalities are useful when projecting profits and breakeven figures. In this OCR Maths study guide, you can revise the more than and less than signs, how to solve inequalities and how inequality can be represented graphically.

Sequences - OCR
Sequences can be linear, quadratic or practical and based on real-life situations. Finding general rules helps find terms in sequences.

Straight line graphs - OCR
Graphs show the relationship between two variables and are often seen in newspapers and the media. People who work in professions involving maths and science commonly use graphs.

Other graphs - OCR
The most commonly occurring graphs are quadratic, cubic, reciprocal, exponential and circle graphs. Their equations can be used to plot their shape.
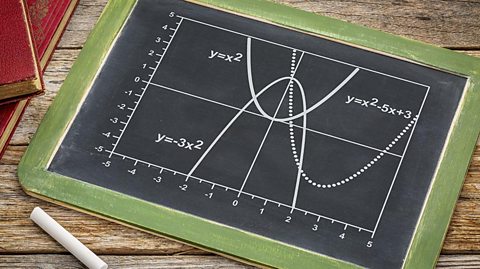
Transformation of curves - Higher - OCR
Functions of graphs can be transformed to show shifts and reflections. Graphic designers and 3D modellers use transformations of graphs to design objects and images.

Using and interpreting graphs - OCR
In real-life contexts, the intercept, gradient and area beneath graphs can contain information such as fixed charges, speed or distance.

Quadratic equations - OCR
Solve quadratic equations by factorising, using formulae and completing the square. Each method also provides information about the corresponding quadratic graph.

Ratio, proportion and rates of change
Ratio in context - OCR
Ratios are seen in everyday life. They can be used when adding ingredients to make a meal, when deciding how much pocket money children get or when reading a map.

Percentages - OCR
Percentages are used in everyday life, for example, calculating discounts during sales and interest rates at banks. Knowing how to find and use percentages is an important skill.

Direct and inverse proportion - OCR
Proportion is used to show how quantities and amounts are related to each other. The amount that quantities change in relation to each other is governed by proportion rules.

Geometry and measure
Angles, lines and polygons - OCR
Polygons are multi-sided shapes with different properties. Shapes have symmetrical properties and some can tessellate.

Loci and constructions - OCR
Loci are a set of points with the same property. Loci can be used to accurately construct lines and shapes. Bearings are three figure angles measured clockwise from North.

2-dimensional shapes - OCR
2-dimensional shapes are flat. The perimeter of a 2D shape is the total distance around the outside of the shape. The area of a 2D shape is the space inside the shape.

3-dimensional solids - OCR
3-dimensional solids have faces, edges and vertices. Volume is the space contained within a 3D solid. Surface area is the sum of the area of each face. 3D solids can be viewed from different points.

Circles, sectors and arcs - OCR
Circles are 2D shapes with one side and no corners. The circumference is always the same distance from the centre - the radius. Sectors, segments, arcs and chords are different parts of a circle.

Circle theorems - Higher - OCR
Circles have different angle properties described by different circle theorems. Circle theorems are used in geometric proofs and to calculate angles.

Transformations - OCR
Transformations change the size or position of shapes. Congruent shapes are identical, but may be rotated or reflected. Scale factors show how much larger or smaller similar shapes are.

Pythagoras' theorem - OCR
Pythagoras’ theorem can be used to calculate the length of any side in a right-angled triangle. Pythagoras’ theorem can be applied to solve 3-dimensional problems.

Units of measure - OCR
A unit of measurement describes one unit of a quantity. Units of measurement can be imperial or metric. They can be converted using conversion factors.

Trigonometry - OCR
The three trigonometric ratios; sine, cosine and tangent are used to calculate angles and lengths in right-angled triangles. The sine and cosine rules calculate lengths and angles in any triangle.

Vectors - OCR
A vector quantity has both size and direction. Vectors can be added, subtracted and multiplied by a scalar. Geometrical problems can be solved using vectors.

Probability
Probability - OCR
Probabilities can be written as fractions, decimals or percentages on a scale from 0 to 1. Knowing basic facts about equally likely outcomes can help to solve more complicated problems.

Statistics
Collecting data - OCR
Many companies and organisations collect data to improve their information and products. Skills in collecting data can make this process more efficient and reliable.

Representing data - OCR
Data is represented in many different forms. Using bar charts, pie charts and frequency diagrams can make information easier to digest.
Analysing data - OCR
In statistics there are three types of average: the mean, the median and the mode. Measures of spread such as the range and the interquartile range can be used to reach statistical conclusions.

Problem solving
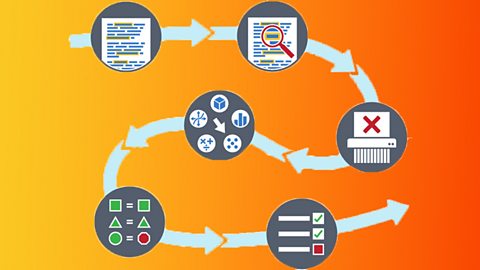
Problem solving introduction - OCR
Mathematical problems cover many different areas of Maths. A framework can be applied to help identify the information needed to solve the problem and to check the answer.
Solving 'number' problems - OCR
Number problems often involve a combination of fractions, decimals, percentages and ratio. They can be set in a real-life context. A framework can be used to tackle these problems.

Solving 'graphical' problems - OCR
Graphical problems will usually be linked to a real-life situation. Travel graphs, temperature graphs and conversion graphs are common graphs. A framework can be used to tackle graphical problems.
Solving 'geometric' problems - OCR
Geometric problems can involve finding the perimeter and area of shapes like triangles and quadrilaterals. Knowledge of shape properties is essential. A framework can be used to tackle these problems.

Solving 'algebraic' problems - OCR
Algebra problems can relate to any area of maths. Problems often include a mix of algebra, number and geometry. A framework can be used to tackle these problems.

Solving 'statistical' problems - OCR
Statistical problems can involve calculating the mean, median, mode and range. Diagrams may include information which needs to be extracted. A framework can be used to tackle these problems.

Links
- External linkExternal link
- SubscriptionSubscription
- External linkExternal link
- External linkExternal link
- External linkExternal link